|
| weblog/wEssays archives | home | |
|
A Fibonacci Analysis of the Housing Market: Where We're Heading (February 12, 2007) Readers familiar with stock market analysis know about the Fibonacci series, and how stock prices tend to rise and fall to levels corresponding to Fibonacci numbers: .382, .618, etc. The way this works is straightforward: if a stock (let's use a fictional one such as Predatory Subprime Lenders Corp., PSLC) rises from $10 to $20, and starts descending, then with a Fibo analysis we can predict the levels it will likely fall to in a stairstep down. We take the size of the move up--$10--and then multiply it by the Fibo series: $3.82, $6.16, and so on (there are intermediate numbers, as well as 1.382 and 1.618.) Next, we subtract that Fibo number from the price peak. Thus our first target for PSLC on the way down is $20 (its top price) minus $3.82, or $16.18. After the stock breaks through that level, we can then look for it to fall to $20 - $6.18 or $13.82. In a full-re-trace, the stock descend back to $10. Since the Fibo series can be applied to any chart of prices, why not apply it to the housing market? Here is a chart of California median home prices over the past 10 years, and a simple Fibo analysis of its price move up, and what we can expect on the way down. 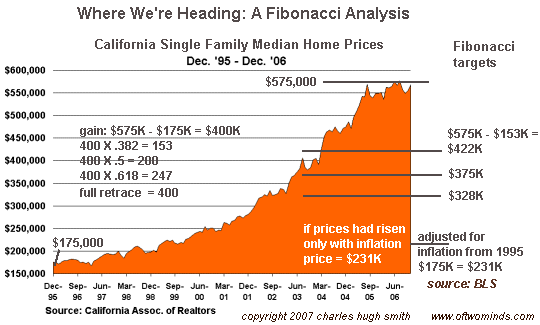
Inflation complicates our analysis. Thus a "new high in the Dow Jones Industrials" in nominal prices doesn't mean the value has returned to its value in 2000--adjusted for inflation, the DJI is still well below its value in the dot-com peak. To keep things simple, I've kept the Fibo targets in nominal (non-inflation adjusted) dollars, except for the starting price. In other words, in 1995 the median price was about $175,000. If the price had risen only with inflation (as defined by the Bureau of Labor Statistics), then the median price would be $231,000 in 2006. If we look out to what prices may be in 2011, five years hence, we have to keep inflation in mind. If we assume inflation continues at a low rate of 3%, then we find that the $175,000 in 1995 would have to be worth $266,000 just to keep up with inflation. If it is worth less than that, it represents a decline in value. Let's look at our Fibo analysis of the future: 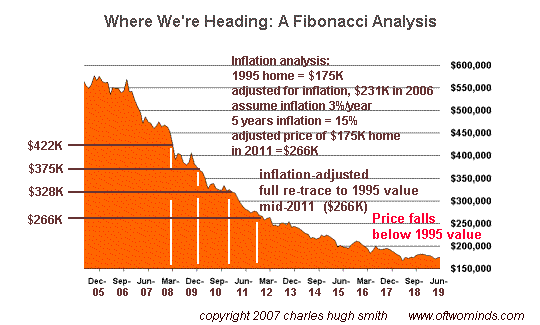
Another feature of price movements is symmetry: what takes five years to rise often takes a similar amount of time to decline. Applying these two simple but powerful concepts--Fibonacci series and symmetry--to the chart of median housing prices in California, we find that in terms of inflation-adjusted value, the price will reach a full re-trace in mid-2011. In other words, the house purchased for $175,000 will have returned to its starting value when the price hits $266,000 in 2011. Should the the price of the house fall below $266,000, the owner is experiencing a net loss in value. While it may give psychological comfort to the owner that the house he purchased in 1995 for $175,000 is still worth (say) $250,000 in 2011, the $75,000 "profit" or "increase in value" is pure illusion. Adjusted for inflation, the owner is under water by $16,000. Yes, a home is more than an investment. But it should still be analyzed with the same rigor as any other investment. If it can't maintain its value when adjusted for inflation, it is a losing investment. For more on this subject and a wide array of other topics, please visit my weblog. copyright © 2007 Charles Hugh Smith. All rights reserved in all media. I would be honored if you linked this wEssay to your site, or printed a copy for your own use. |
||
| weblog/wEssays | home |